分享2个超实用的线性回归分析操作教程，有手就会！

数据挖掘有很多重要的方法，线性回归分析就是其中之一。我们在高中和大学都有接触过线性回归的概念，这里就不赘述了。本文也不会涉及到有关数学理论方面的知识，还是以应用场景、操作方法的介绍为主。

一、应用场景：

首先，一起来了解一下线性回归分析的作用。在我们的日常生活中，线性回归分析是会被常常用到的。运用线性回归分析，我们可以了解到两组数据间有没有存在相关性。如，当我们想知道广告费用的投入对销售额增长的影响程度时，就可以运用。公司应不应该加大广告费投入，如果未来投入一定的广告费用，预测销售额可以达到多少…这一系列问题都可以通过线性回归分析去得出答案。

线性回归分析方法运用的前提是要具备两组以上的数据，然后就可以开始应用检验啦。下面给大家演示一下线性回归分析的方法、操作过程，用到的工具是Python。

二、Python实现过程：

第1步：数据导入

首先要做的就是把本地的EXCEL或者CSV文件读取到Python里，我们可以引用pandas库去读取数据：

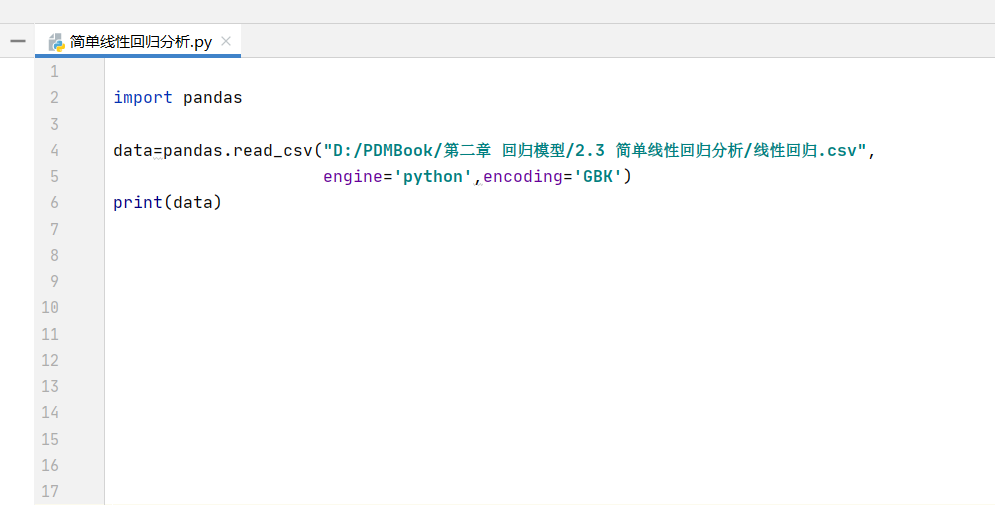
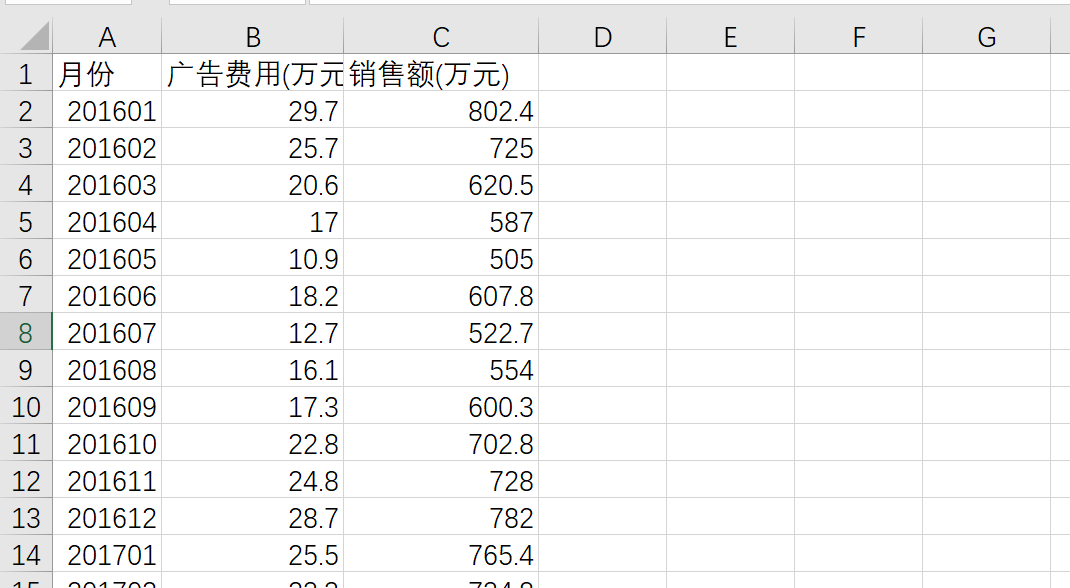
待数据读取成功后，我们需要对数据进行确认，用到的方法是将打印数据与EXCEL数据进行对比：

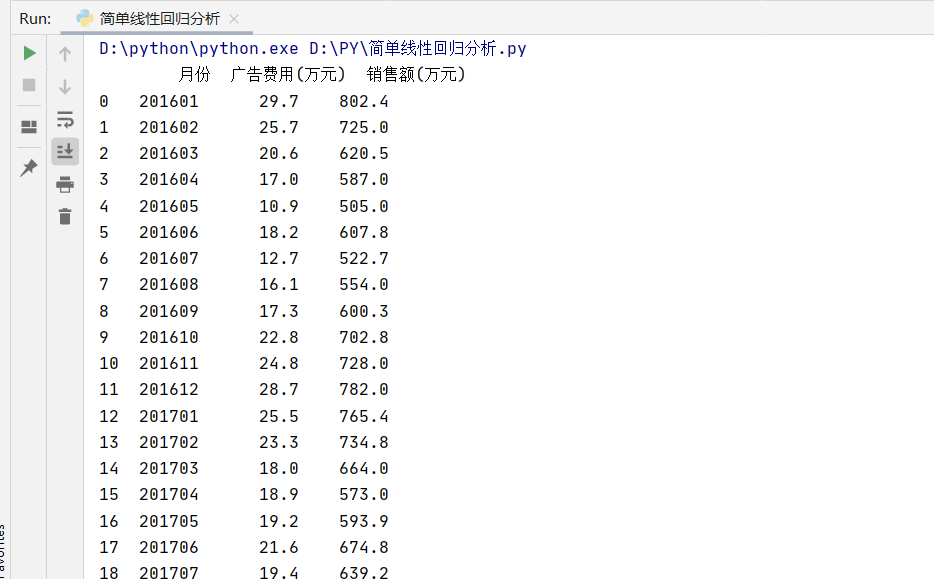
第2步：计算相关系数

如上文所说，线性回归分析的前提是要有2组数据。在数学上通常是用皮尔逊相关系数来进行检验，这个数值越接近1，就代表两组数据越具有相关性，我们可以用corr这个函数来对广告费以及销售额进行检验：

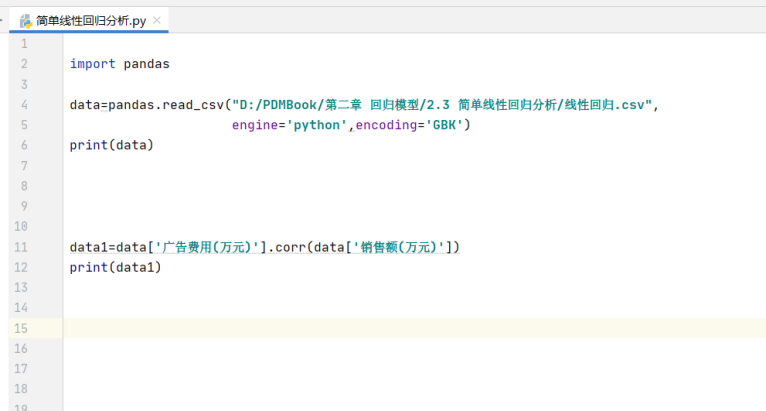
然后，打印data1，可见相关系数的值就已经得出了。数据为0.93，与1非常接近，有数据可知这2组数据的相关性是非常高的：

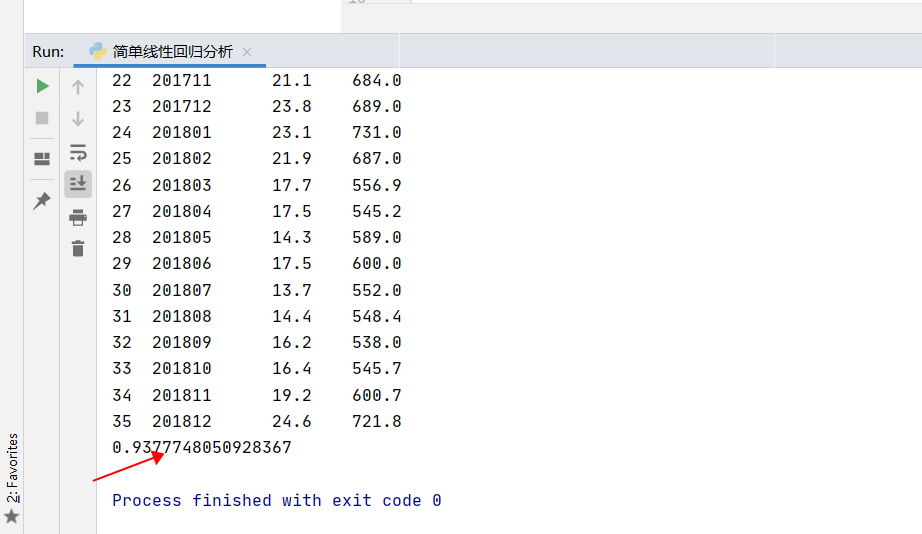
第3步：画图

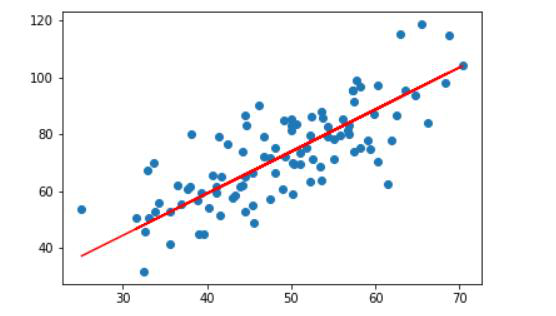
为了更加直观地对这两组数据进行呈现，我们可以画一个散点图，接入matplotlib，X轴为广告费用，Y轴为销售额设置。接着利用plot（）函数来画图，最后利用show（）函数进行图表呈现：

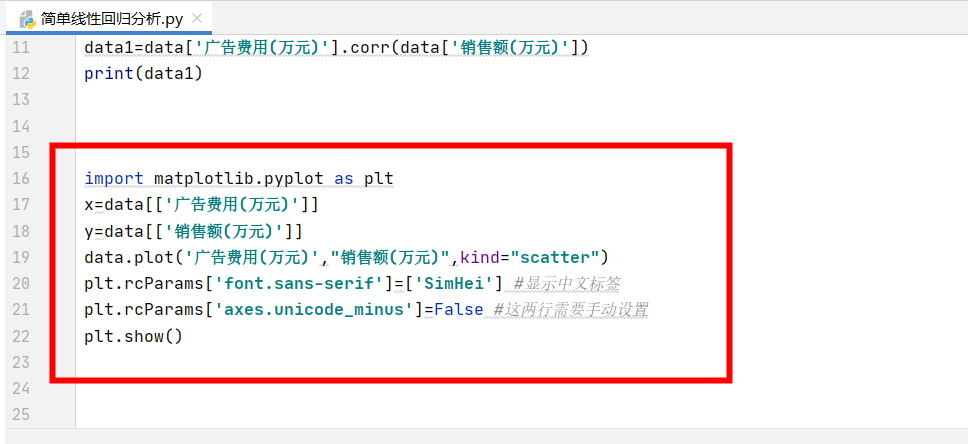
打印一下，我们看看图形的效果，从图中可以看中，散点图点排列基本在一条直线上的，由此可知广告费用与销售额是呈正相关的，广告费用越多，销售额也会随之增长，这也对我们上面计算出来的相关系数提供了一个非常好的佐证：

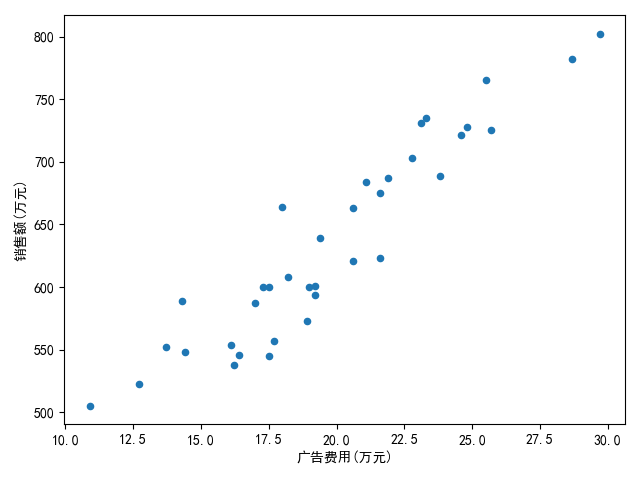
第4步：建立线性回归模型

用y=ks+b公式表示线性回归的方程，X为自变量、Y为因变量、K为斜率、b为直线在轴上的截距。接入sklearn库，对着上面的数据建立线性回归模型，sklearn库主要是进行机器学习。先利用LinearRegression()对象定义，再利用fit（）函数对X、Y的值进行模型训练，最后输出coef_，代表k值、是intercept_，代表b值两个数据：

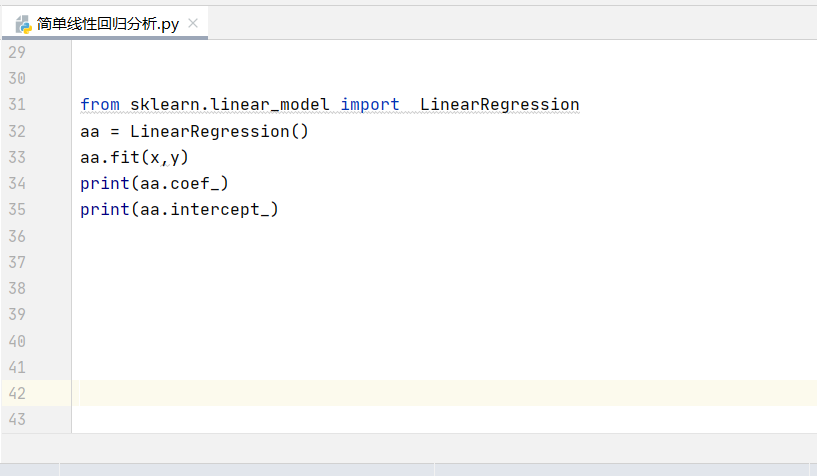
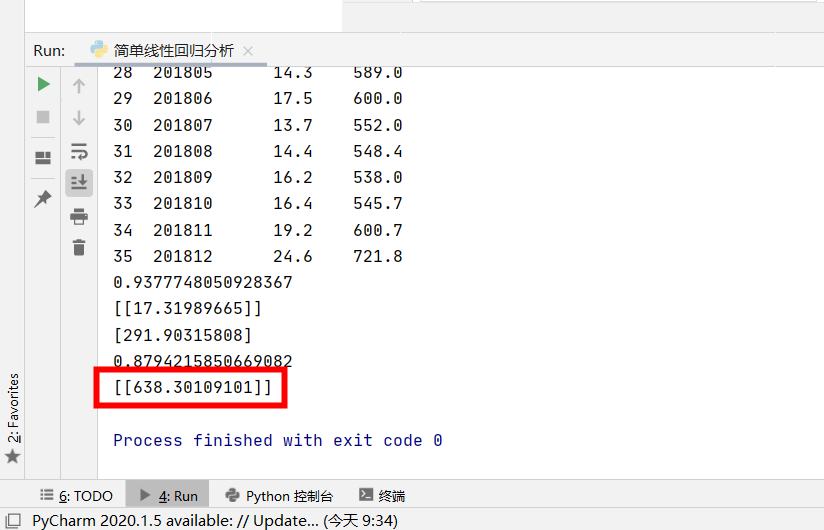
输出后的数据如下，k是17.3，b是291.9：

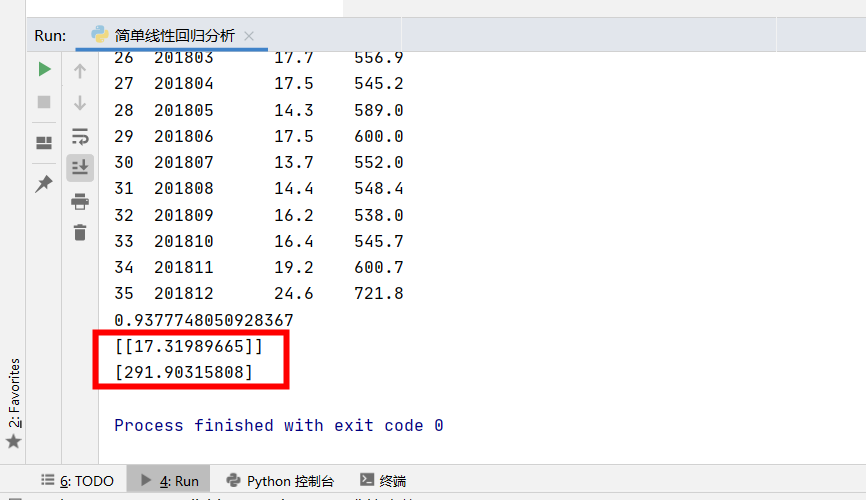
利用score（）函数对模型的拟合程度进行检验，当数值越接近1，就代表该模型的拟合程度越好：

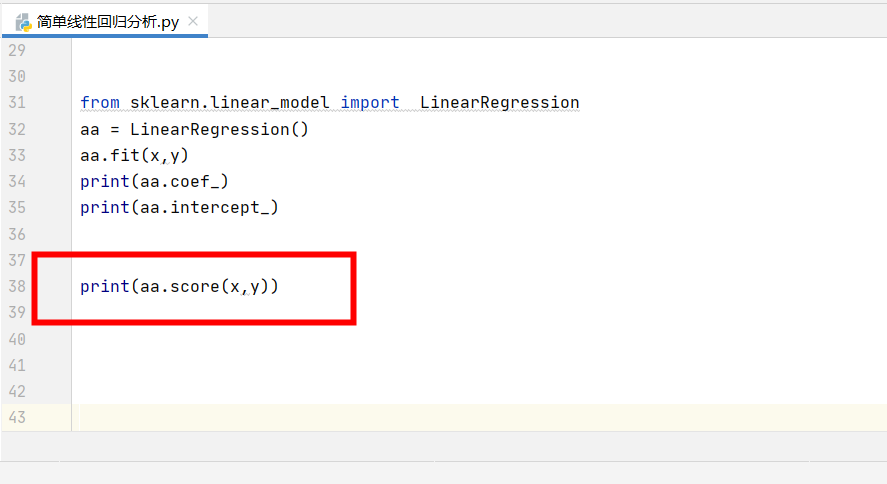
计算结果出来了，0.879，已经非常接近1了，可见模型的拟合程度很好，能投入到实际应用中去使用：

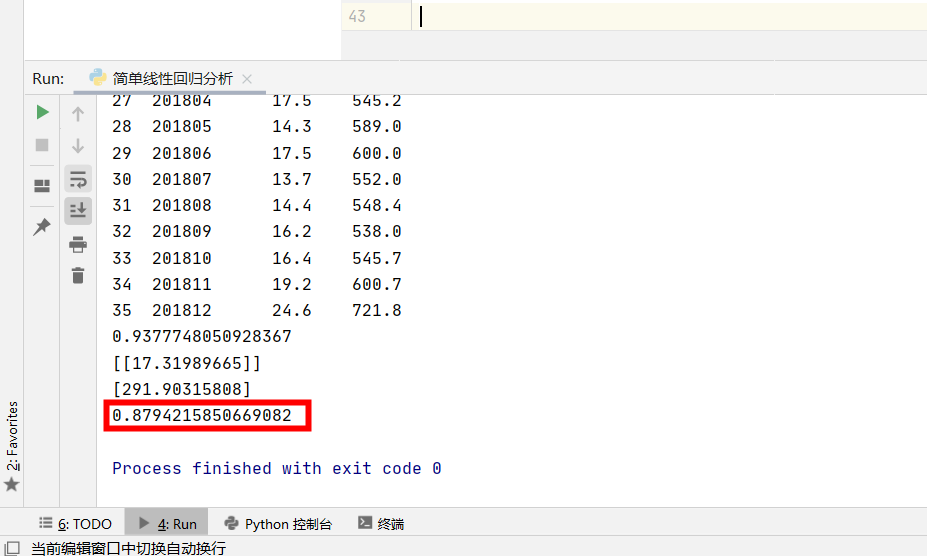
第5步：数据预测

k和b的值也出来了，现在只需要x的值就能够推算得出y值数据，现在我们可以利用这个原理去对数据进行预测。这里可以利用predict（）函数接入一个参数对数据进行预测，例如下面我们看看广告费在20万的时候，销售额预计会有多少：

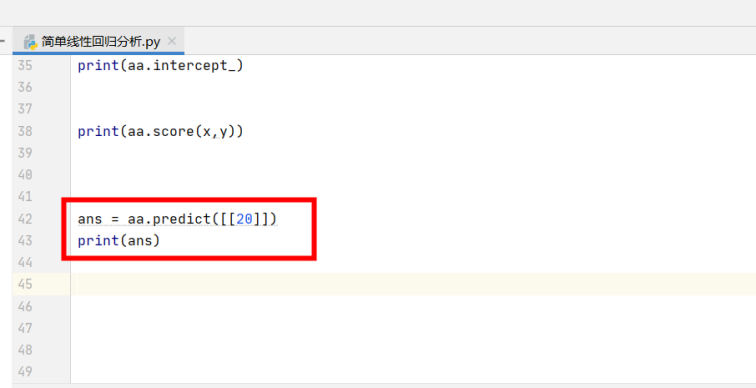
最后算出来的销售额是638万：

三、后续建议

从python的实现过程来看，通过写代码的形式能够实现线性回归分析的整个过程，但是毕竟大部分小伙伴都没有接触过这门编程语言，如果真要用python去做的话可能会难度比较大。那么有没有更加简洁一点的方法呢？当然有！再给大家介绍一个更加简便的方法，用到的工具是smartbi。

当前界面为数据挖掘界面，工具栏位于界面的左边，可以看到工具栏上的组件有很多。这个也就是ETL工作界面，ETL常应用于数据清洗上。ETL的数据源治理能力非常出色。如果把ETL和数据挖掘结合起来，必然可以大幅提高数据分析的效率。

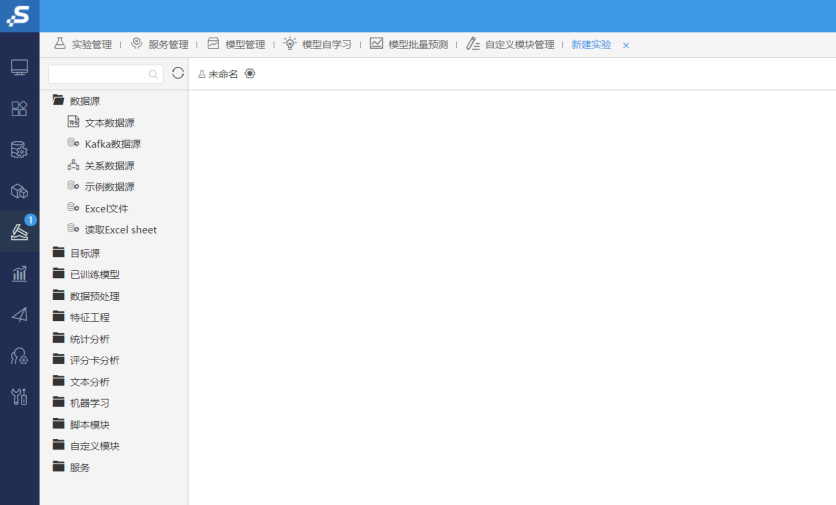
第一步要做的是先把数据源读取到ETL的界面里，我们可以把EXCEL文件这个组件拖拽进来，并把上面的广告费用的EXCEL文件读取进来：

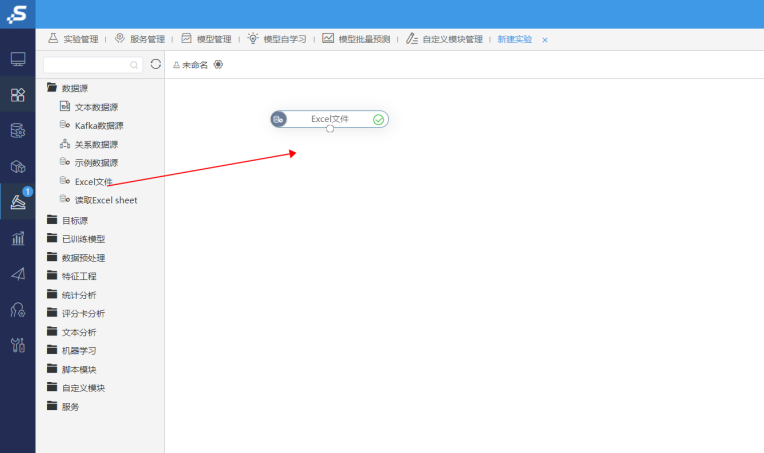
如果EXCEL文件中存在着多个sheet，还需要把读取Excelsheet这个组件拖拽进来，并读取您的目标sheet：

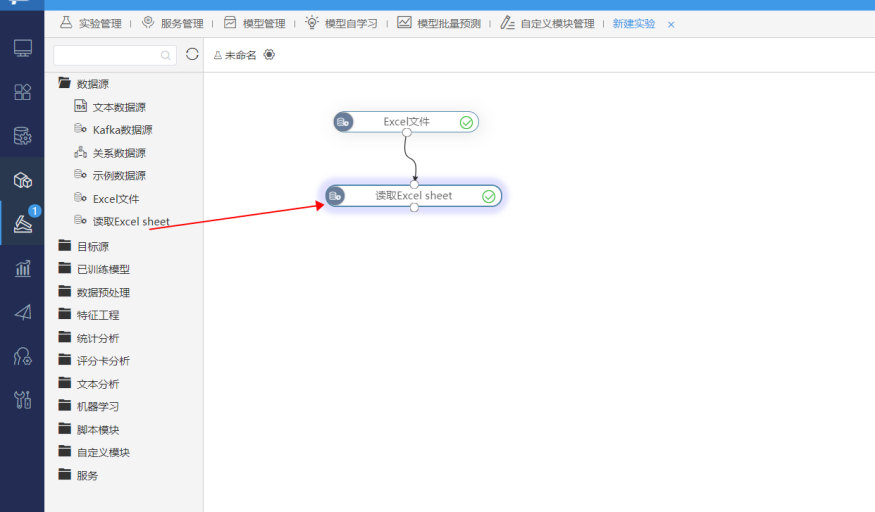
完成数据读取后，预览数据源:

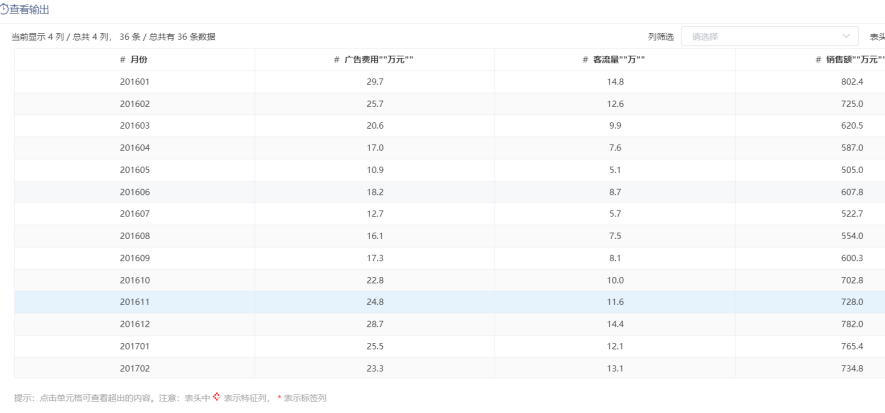
接下来是广告费用、销售额的相关系数计算，将相关性分析的组件拖拽进来，将其和上面的组件进行连接：

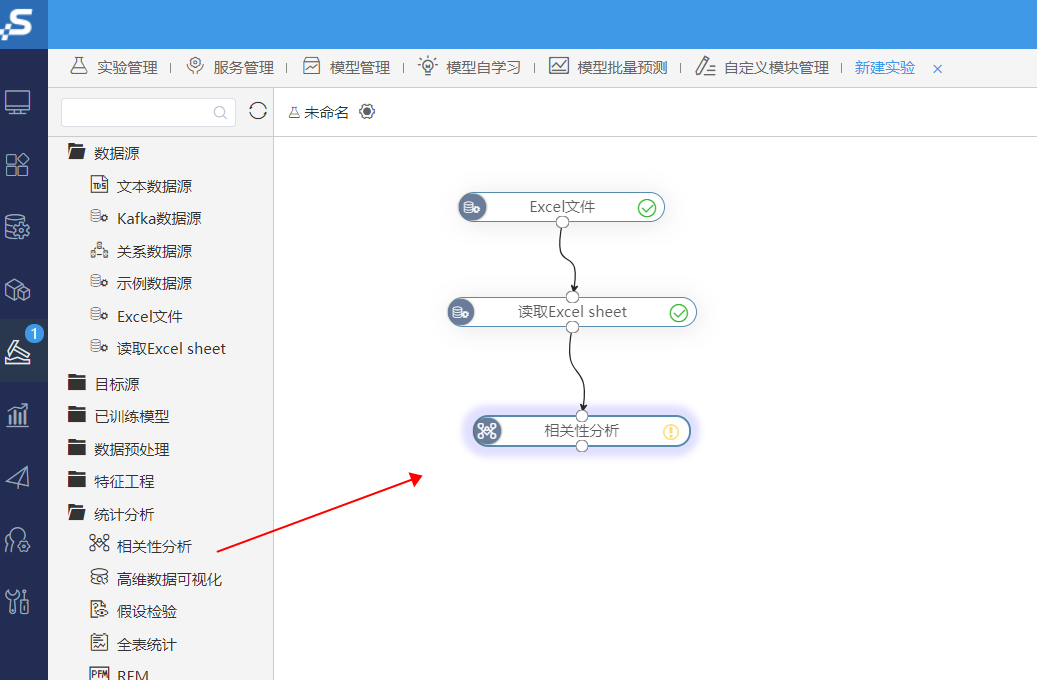
鼠标选中相关系分析，在右边的待选列里把销售额和广告费用选中，并移动到右边：

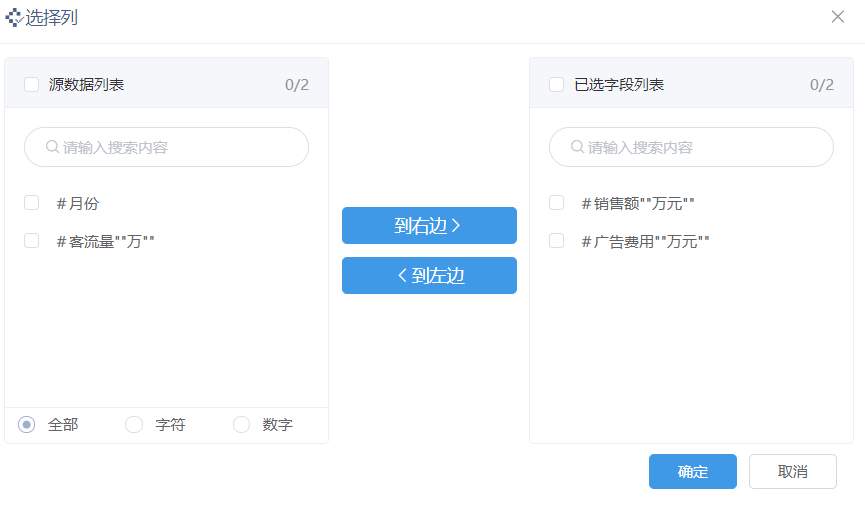
查看输出效果，只需要点击广告费用、销售额的中间区域，相关性系数为0.94。该数据与Python计算结果一致：

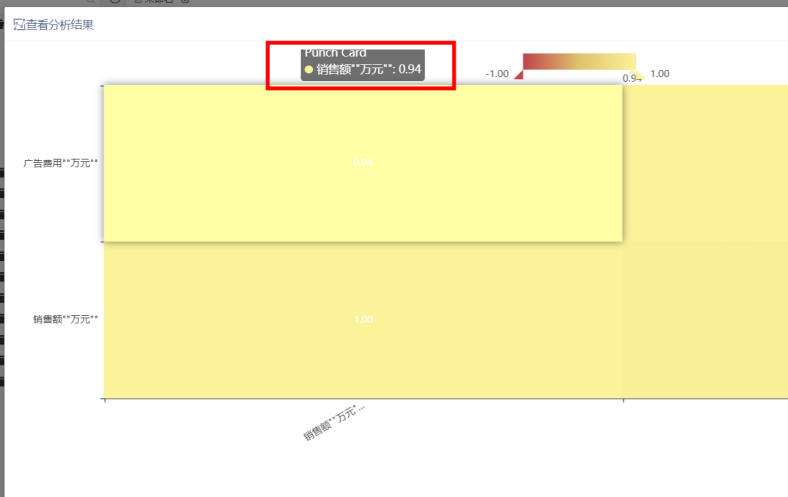
由于篇幅有限，散点图、数据预测等其他功能实现的方法就不多做介绍了，有兴趣的小伙伴可以自行去研究一下。

申请试用